Modernism, Postmodernism, and Digitality

The shape of a convolution in History

A Convolution of History

If you look for Convolution on the Internet you will see a tremendous number of people who are engaged with math and who are engaged with physics specifically the physics of signal processing. The problem that we have here is that this is a new area that has not been exposed to the idea that convolutions are needed for the study of history. It also means that the kinds of Convolution that are interesting in physics or engineering are not the same ones that we are interested in.

To review:

1. When one looks at a historical era governed by a Cultural system one can with some difficulty chart the cultural era by a sigmoidal curve.

2. This is because of the Population Pyramid and its reproduction by Dirac Delta functions.

3. The reason for a Convolution is to show why a cultural system is necessary in mathematical terms.

4. Therefore the logical form of a Convolution will be one which is like a sigmoidal curve.

Fortunately, Convolution Is in the end an operative like + or / - needs only to arrive at the right inputs to reduce the right output. Therefore be first step is to understand what a coalition does in a graphical sense. Engineers think of this as an input and a response though they admit that either function can be the input. They are terrified of the mathematics of it but they are interested in the signal that is produced and not what the mathematics means. The engineers are also interested in a spike, similar to a Dirac Delta spike because they are interested in a signal which is only g(x) with the f(x) function being the spike. For the engineer this is sufficient. And because of the commutative property, they know that whichever one they select as input the other one will be the output.

Unfortunately, as historians mathematics is intensely why we are doing this, and instead of having a signal which is g(x) the historian once two functions which are different and produces a third one that is different from either of the other two. What this means is that we have to figure out how to produce two functions, one that is stochastic and the other one which is kurtosis: One which reduces all of the living and dying and the other one which produces ideas, cultural similarities, and copying of others which makes culture possible.

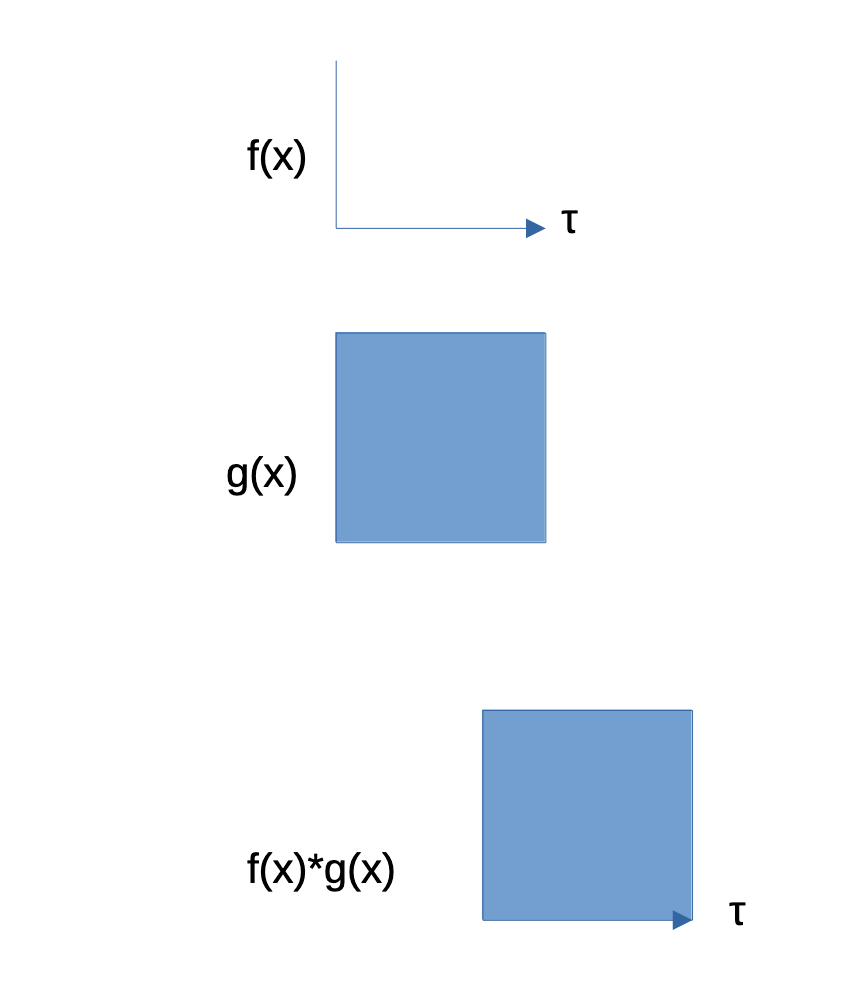
So the first step is to show the basics of convolution. This means that for f(x) a Dirac Delta function and for g(x) a square.

This produces the following:

The spike moves through time, and the response is of g(x) and is, in this case, immediate. Which produces the figure at the bottom: a g(x) along the time dimension.

While this is useful for describing the population of people in a population pyramid, it is not sufficient for describing how a Cultural system moves from being visionary, that is the idea is present but there is no support from a wave of people who need this cultural system to explain and produce in the real world.

That means that we must alter f(x) and g(x) to contain the two functions that we need. However, the f(x) is similar to the derivative: after all a population spike occurs when a large number of to Dirac Delta Functions are clustered together to produce a wave of children. This means that we can extrapolate how a baby boom proceeds. It proceeds when there are a large number of adults who work close together. This is what happened in 1940 when the United States put into production war materials for the Allies and built up their own resources because it was obvious to the commanders and politicians that war was going to come to the US. This means that for the stochastic function, we can alter the shape of g(x) to mimic what happens when babies are born in close proximity. The fact that there is some difference is shown by how the children grew up in what was called Project Y at Los Alamos, It was described as a boomtown and a city. Over one1/5 of the married women in 1944 were in some stage of pregnancy.ⁱ

This means that we can take the Dirac Delta function and by substituting a human life for g(x) and then multiplying those in a short space of time, which is what convolution does, we can see that the stochastic form is already duplicated. This means that we have an output that forms the population pyramid, And now we have to form the other function of creation in a particular cultural syntax.

But this means that we can have as many Dirac Delta functions, so the g(x) is composed of a convolution of several DD Delta spikes which form a population explosion. remember we can have as many as we like of a particular input. since we do not know the exact shape, unlike physics, we can do the next best thing and use a Gaussian shape with sufficiently large error bars.

The next step is to form the kurtosis, and instead of using a signal processing form, we go to statistics.

i Shea, Patrick. 2024. “ life on the ‘Mesa’”, Scientific History Institute Museum and Library, Philadelphia.