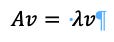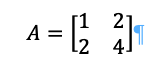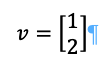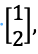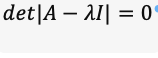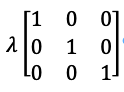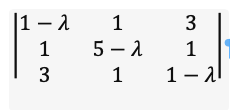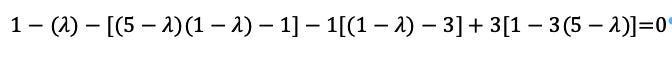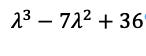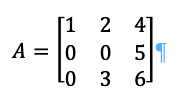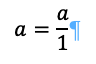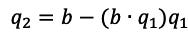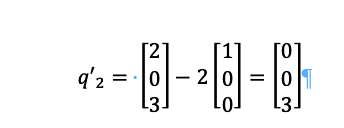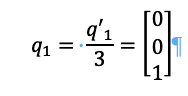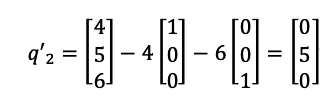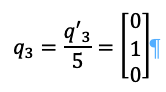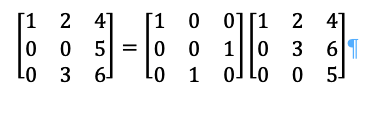Eigenvectors and Eigenvalues
This why we have chosen Linear Algebra to represent the data and now here is a point that that choice comes with a cost: we must compute “the eigens” namely eigenvalues and eigenvectors. What are eigenvalues and eigenvectors? Eigen is German and in this case, it means “characteristic.” Since we are dealing with vectors and matrices of vectors this means that the eigenvector is the direction of a characteristic vector in the set and the number associated with it is how far the scalar part extends.
A simple example is imagining a painting that has been shifted to another form, if the vector has not changed it is an Eigenvector and otherwise it is not. Eigenvectors and Eigenvalues together make up the Eigensystem. If it has a function, then it is called the Eigenfunction. So, for a painting that has been warped in some way then the Eigenfunction tells you what the Eigenvector and Eigenvalue will be. This means that it can be written out as a matrix A, so long as there is a non-zero vector v:
Where A represents the matrix, the v represents the eigenvectors, and the 𝜆 represents the eigenvalue. Every eigenvector has an eigenvalue.
The key concept is that eigenvectors are not rotated. For example, suppose we have Ax:
Resulting in:
That means that v, in this case, is an eigenvector
and the eigenvalue is 5.
This means that the eigenvectors and eigenvalues are related by this simple equation, if one knows how to get the eigenvectors and eigenvalues. This is not difficult but requires some practice. It is a practice that history majors do not get because there is no need for vector algebra in the form that the discipline is taught. Of course, this book is going to change that because, as Lord Rutherford is said to have remarked “That which is not measurable is not science.”
Let us take another example, imagine:
Which satisfies:
Where I is:
What are its eigenvectors and eigenvalues?
First distribute the -𝜆 down the diagonal by subtraction:
Then multiply by the determinate, again on the diagonal:
Or:
Simplifying that means:
We do this for several reasons, for example, the sigmoidal curve that describes a Cultural System does not play out in exactly the same number of years each time, so when we are going from raw data to showing how the sigmoidal curve plays out in particular circumstance the “A” of the data is the actual data points, and the at the end is the normalized version of the sigmoidal curve. This means that the data with years is put in and the curve at the end comes out. This means that the raw data is transformed into the sigmoidal curve and then one can place a signal as a marker.
For example, in the sample, one of the most recent markers is the Covid outbreak. The raw numbers need to be transformed into a marker. The first step is to transform the deaths so that we can see that in proportion to the total number of deaths that Covid stands out as a contributor far beyond any assorted other kinds of death. And that means changing it from “A” to “ 𝛌” by this means. The major problem is that the determinant is not a simple multiplication or division but trades on the fact that it is the diagonal after the row and column is taken out. If the audience for this was physics students and professionals, this would not have to be done since Vector Algebra would have already been taught to the readers.
Key Points on Eigenvectors and Eigenvalues
1. The algorithms for finding eigenvalues and eigenvectors need to be memorized.
Gram-Schmidt Process
This is a section which is done far better in far more places. However, because it is such an important aspect of writing Cultural Systems in a historical mode, it needs to be explained at least in some detail. The Gran-Schmidt process is meant to decompose factors into an orthogonalization group of vectors. This means that we are taking vectors that have been observed by whatever means is necessary and converting them into two matrices which when multiplied together will equal the original value. One of these matrices will be orthonormal and the second one will be an offer right triangular matrix.
So in math if A is the original matrix of vectors, and Q is an orthonormal version of that matrix, R is the upper right triangular matrix, and if A is the given, then:
A=QR
The process is rather simple but grows more complicated based on the conversion of Q and R. The idea is to take one of the factors in A and establish this as the core vector which everything will be ordered around. Because time is often one of the vectors, this means that time may be the vector even if it is not the most convenient one. Then take each educational factor and multiply this vector times all of the preceding vectors until you have finished. This will give you Q and then you must calculate R to make it so that QR is equal to A.
Let us take an example: using three vectors let us take:
Knowing that this is a very simple matrix and will not engage in too many square roots etc.
Let us label the three columns as a, b. c. this will give us:
And let us take q1, q2, q3, as the orthonormal results of a, b, c.
To generate q1 we simply take:
Because there are no other columns and 1 is the length.
Then we take column b:
Let us take two steps, taking q2 and then orthonormalizing q1 with respect to q2.
Then:
And finally, we take q3:
Or:
Then ortho-normalizing:
This means that:
This is the first step.
The second step is to compute R:
But since Q is a permutation matrix which means that:
∴
This is important for calculating the sigmoidal curve, where A will be the data from actual measurements, and to will be the sigmoidal curve with R being the exchange from the actual data to the sigmoidal curve.
The next step is to use Singular Value Decomposition, only instead of breaking it in two to matrix QR, we are going to break it into 3, with two of the matrixes being inverted. This means that R is broken in two to matrices.
Key Point on Gram-Schmidt Process
The Graham-Schmidt process is extremely useful for orthonormalizing data into various configurations including sigmoidal curves.