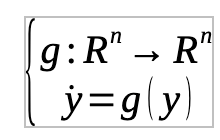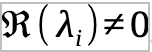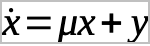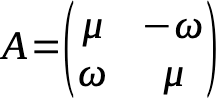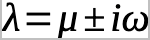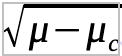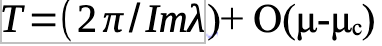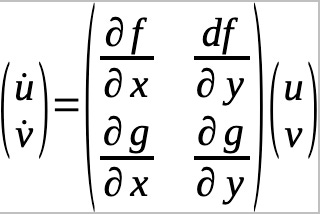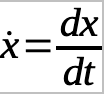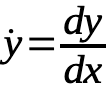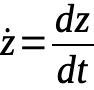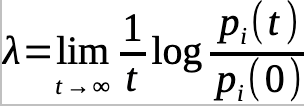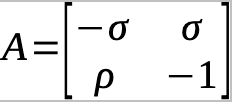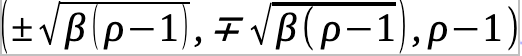Xaos in History
It might seem as if this was unnecessary to use mathematical concepts in history. But there is a larger point that now needs to be explained: having to find people, ideas, and objects in history as vector space parameters we can then use the mathematics of vector spaces: that means Singular Value Decomposition, Primary Component Analysis, and Xaotic distribution.
These three stack in our path to show that history can move in deterministic but unforeseen ways at the Cultural Systems level. This is akin to neuro-networks in that it takes a number of dimensions, called a basis, and looks for those measurements which have a high degree of correlation. Basically, we look at history to find that there our myriad variables but only a few really determine the variance in one particular range. This means that there will be multiple logical systems, but we are only looking for the patterns that have variance in one logical system.
This means defining Xaos Theory in such a way as to be generically useful.
Bifurcation
Up until this point we have used linear algebra in a very straightforward way which an undergraduate would immediately see as like problems in physics. It may mean that the linear algebra may be straightened but very little beyond that. This means that when taking averages of a vector it is trivial to work out the vectors and it is only slightly more complicated to realize that even though there may be many vectors only a few will drive certain problems, and the rest may be discarded. When we started to study PCA it became immediately obvious that a small number of vectors had a large weight in proportion to the direction of a vector space. This means that whatever Cultural System that you are making the first step is to find out which PCAs have this effect in your particular system.
For example, we then looked at the average of a vector, for example, the ratio between black and white and color television sets. But the key aspect of Cultural Systems is that they are Xaotic. This is immediately present from the Dirac delta function and proceeds onward with many punctuated functions being of the same sort in that they immediately affect.
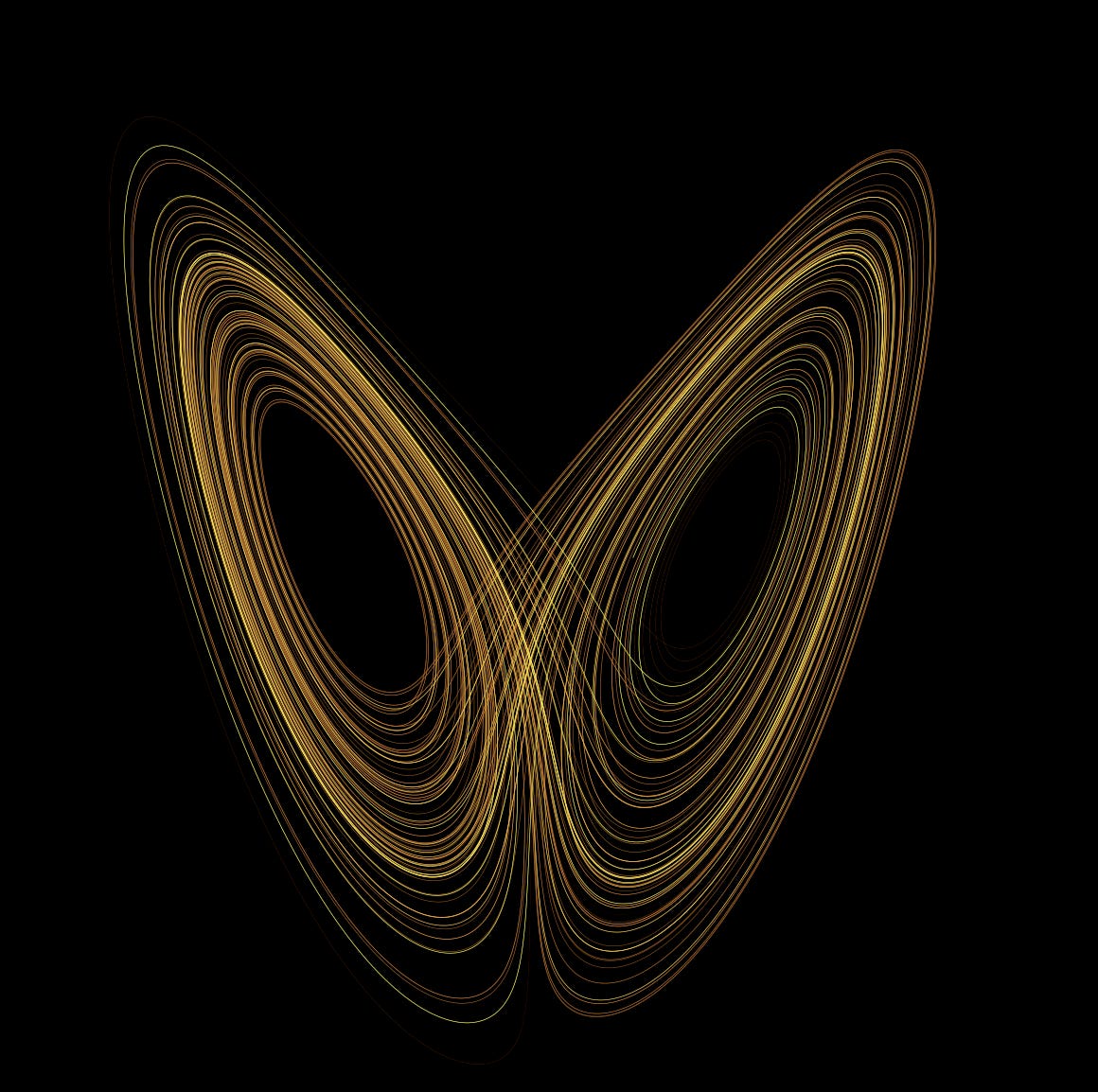
Some of you may have a structure known as the Lorenz system. This is an example of bifurcation around two strange attractors. One of the purposes of using linear algebra is that it can form a such system and offer key points as to the structure of that system in action. But the first point is to understand what bifurcation means in a Cultural System and why it is important in a historical context.
The key point of Xaos Theory is what is called “bifurcation” which in itself merely means that a point or an area is divided into two separate parts. But more exactly when the oscillation of a given event can go one way or the other and the definition relies on the fact that on the real plane, there is a fixed point that is “sturdy” and will not change without some effort. For example, the point that New York City will not change, and even the aspects of New York City will change only with strong forces such as the shift from London to New York as the center of finance. But given this center of finance, one can look for signs that it is so bold in terms of printed material but also manufactured goods. This means that an abstract sign can be seen in tangible goods.
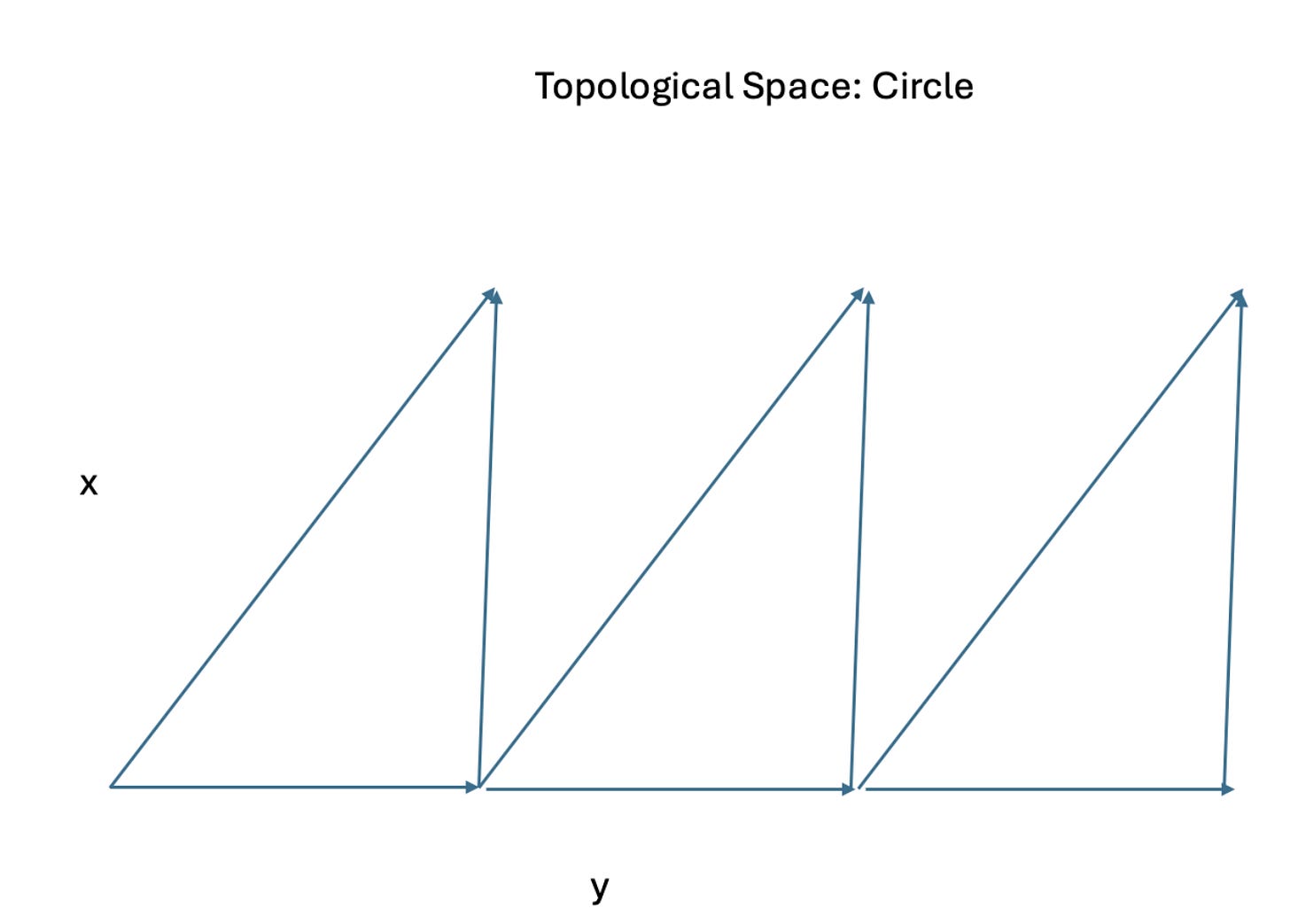
We must then prove that in a topological sense, the dynamical system is both transitive and equivalent. A topological system means it is continuous and it is a metrizable or in another way, there can be some form of metric space, though we do not care which one for the time being. That means that orbits must be continuous once drawn. But that means that it may be discrete and foldable. So, for example, a circle can be a discrete topological system if one holds it together at some point.
The nature of the definitions is fluid but transitivity means that the orbits are dense and are infinite, and equivalent means there must be a homomorphism. If both of these conditions are filled, then it is Xaotic in this sense. That means that we must introduce typology to make certain things clear.
The primary two motivations are:
A way to quantify the sensitivity to initial conditions. For this, we shall introduce a concept known as the Lyapunov function.
A way to show that there is a density to motion that can be described. For this, we shall use Jacobian Matrixes.
Then we shall combine the two to produce a general method of identifying when a system needs to be Xaotic.
This means that a Xaotic system can be put in place in any vector space if the vectors. If we want to approach the origin point in a dynamical system, then we must use a Lyapunov function. This center in history can be defined as the point of stability that the entire system tends towards but does not ever reach. Instead, various groups of people center around the Lyapunov function trying to reach it but finding that other groups of people do not want the same equilibrium that they do. For example, in a democratic parliament, there will be a series of parties each one trying to reach the center but having to deal with other parties which want a different center.
First, we need to define the Lyapunov function, the problem here is that the name is spelled differently by different people, and I chose this one because it is how it was introduced to me many years ago. In ordinary differential equations, Lyapunov is a dynamic system where:
Is a scaler function.
That has an equilibrium at y=0
g(y) >0 for y ≠0
Defined on a region that is positive and continuous.
Has a first-order partial derivative at every point in that region
g*(y) is the dot product g*(y) = 𝛻(y) ⋅g(y) for g’ = g(y)
why this is important is that the left-right distinction at any given moment is related to the other individuals, but over the space of time, these points move based on the different solutions to exigent problems.
This is sufficient to prove item 1. Because if the Lyapunov exponent is present then the sensitivity to initial conditions is also met.
But there is also number 2. In Xaos theory, whether it is on a line or a number of dimensions the same mathematics holds for bifurcated regions but with changes if the dimensions are greater than or equal to 2. This means that we can examine the single line and then go forward from there. A fixed point is hyperbolic if the eigenvalues of the linearization all lie off the imaginary access, or
for i= 1 … n. this means that the phase portrait will be structurally stable if its topology cannot be altered by a small change in the vector field.
The key to Xaos is that it is in partial differential equations so we must use a symbol to represent the change and the common way is to use “ẋ” and so on. For example,
where equals a control parameter in growth. This means that if μ>μc , where c is the critical value of bifurcation, it grows larger, and if μ< μc , it grows smaller. That is μc is the bifurcation point. In the language of Xaos, this is called the supercritical Hopf bifurcation. When this happens a stable spiral changes to an unstable spiral in dimensions n≤2.
Here is where we discover that the eigenvalues are a key point to the behavior of the spiral. If we rewrite the system in Cartesian coordinates, then we can more easily find the “Jacobian” for the system. A Jacobian in this case means a Jacobian matrix which we then use to take the terms of linear algebra. That means that the Jacobian is a matrix so that, as an example,
Which then has the eigenvalues:
This means that the supercritical Hopf has a Laplace transformation rather than a Fourier transformation. It means that there is not only an act that other people can perceive but there is an inner act that only the individual can perceive.
As with any Hopf bifurcations, there is an idealized limit cycle and a more practical one. Ideally:
The size of the limited cycle grows continuously from 0 increase proportional to
for μ close to μc
The period is:
where is the imaginary plane
and O(μ-μc) means quadratically small components on the terms - though this needs to be defined in each specific case.
However, history is particularly given to artifacts because we do not know all of the details only those which have been preserved in some way. This means that the shape is distorted and often made “ghostly” because of the sparsity of data.
Let us take an example: consider people who rent housing in a particular urban area. There is both a monthly and yearly cycle that can be shown by rental agreements. This means that we can draw a Hopf bifurcation with an inner cycle and an outer cycle which shows the payments from one group of individuals to another. It also shows that some individuals do not have payments and leave the loop. This means that there is a homeomorphism that maps a loop, and a time direction is preserved.
This means that one can construct loops with closed orbits if they are structurally stable with tiny movements to the field. If movements of the field however can be changed even by small perturbations, then the point is not stable as mentioned above in the general case. An example of this would be countries that are not at war: there may be small violations between the two nations but not by the nations themselves. If, however, the nations tilt over into war then the structural point is not stable. This is what war means: some form of negotiation must be entered into before the two countries will have normal relationships. This means that we can divide a particular Cultural System by which members are important to that Cultural System. Because the nature of warfare is unstable, we can then look for stability versus instability.
This also means that Xaotic perturbations may have a limited time or an unlimited time. This means that there can be subcritical, supercritical, or degenerate bifurcation. What this means from the Cultural Systems standpoint is that in a given Cultural System does the Hopf bifurcation exist in the Cultural System? For example, payment by one party to another for specific work done during the period would largely be within a Cultural System. But when “giga work” is introduced, it violates many of the conditions for work for hirer, as do zero-hour contracts and similar conditions. If these are unstable from a topologically equivalent standpoint then they will have fixed points which are also unstable. These may be forced by employers on their employees if there is too much work for traditional employer/ employee contracts. And one could explore whether or not these contracts are mutually beneficial or work more towards one party or another. If they are unstable then this would be shown by the Hopf bifurcation.
What this means is that near a strange attractor, there will be a Lyapunov exponent which differentiates the sides of the bifurcator because if it has sensitivity to initial conditions it must also have a Lyapunov exponent.
This means that the Lyapunov exponent is equal to the quadratic functions if they do not converge together and are dense. That is, if the quadratic functions merge together there will be not a Lyapunov exponent and if the quadratic functions do merge together then there will be a Lyapunov exponent that divides the bifurcation in a typologically transitive way. This means that it is Topologically equivalent and therefore has a homomorphism.
What this means is that instead of a straight line, we must linearize the system. To do this we take u,v as the disturbance so that O(u2,v2, uv) denotes the quadratic terms in u,v with the Jacobian matrix linearized at the fixed point (x*,y*) and this makes u,v arbitrarily small:
This means that there is no Lyapunov exponent on these arbitrarily small terms. This means that if u,v are not one of the bifurcation points there be no Xaos approach at that point.
This means that we must find a bifurcation point. Since this is history rather than any other discipline, the way to do this is by showing that there is a Fourier transform in the immediate consequence. An example would be a meeting, and the decision points arrived at by that meeting are different from possible decision points. An example is the moment when instructions went out from a meeting in the wake of the First Battle of the Marne which is different from the decision to have some kind of resolution in negotiated terms. In other words, find the meeting that has made a decision to continue fighting rather than sue for peace. This makes it very clear that Cultural Systems still need to be analyzed in words and then translated into numbers. It is the numbers that will show whether bifurcation has occurred, but the words are how those numbers are created. But because there are Fourier transformation points, such as the purchasing of an object which is a transactional event that can be quantified, it is similar to a biological event in that the biological event can be translated directly to numbers. This will explored later.
Further levels of rigor may be explored with a more detailed explanation of whether the order line case is a center, to generate nodes, stars, or other divides.i This will be dealt with in the next section.
Again, we must underline that time is a recursive function, not merely a value to be incremented. This means that the development of a bifurcation will occur at a specific moment. An example would be a tropical depression: there is a point when the bifurcation develops over time. When this happens, the bifurcation becomes quasi-stable. This may mean that in the long term, it is unstable, but that it requires another change. In many cases the change the overland but this is not the case when in the Eastern Pacific the bifurcation simply runs out and is no longer able to produce a bifurcation. Remember that the bifurcation must be stable for this to continue indefinitely but it may continue for a long time as a quasi-stable bifurcation.
In the Hopf bifurcation, there is a stable and an unstable point around the access meaning that there are three points: the two bifurcations which are linked, and the origin point which is the centering of the condition.
This means that while the Hartman-Grobman theorem applies, it must still be a translation from words to numbers.
One point about History is that it is Xaotic the proof is found in several ways, but the essential point is that the Gaussian curve acts on both the standard deviation and on the kurtosis. The synopsis of the proof is that the kurtosis on the upper end produces Dirac Delta Functions which act on 𝜑, that is the mean of the population. But the kurtosis acts at a Xaotic interval so that the kurtosis acts at a Xaotic time to produce a Fourier Transform which acts on 𝜑 in a Dirac Delta Function that produces a Lyapunov Exponent that is Xaotic.ii
That means that at any given point in time, there will be a left/right division that moves over time around the Lyapunov point. If we center the basis around the primary component analysis for the “political center” but realize that the center will change over time, then the PCA can mark the center at any given time even if the changes become quite large. An example would be the “Democratic party” in 1920 is different than in 2020, though both would be regarded as “left” in the context of the era.
This means that a Xaotic System can perhaps form a Cultural System where each individual perceives a center point around the Lyapunov point. Each group of individuals will then try to move towards the center point but has the problem that other groups will move to counter avail. For example, the extreme right of the Republican party in the United States believes in a MAGA platform and tries to eliminate foreign aid which seems to them to be superfluous. Other groups have different opinions, and the dynamical system can be plotted by looking at the votes of the individuals in the House of Representatives and in the Senate. Since in order to get something passed and signed into law requires a consensus, the Lyapunov point at any given time can be seen by which bills are passed. Because the access is from left to right, we can model it by a PCA taking the primary factor as left to right and the cofactor as differentiations for other reasons.
But remember that the system is Xaotic and even though the form is deterministic, small changes will produce arbitrarily large differences in a very short time. This means that a Cultural System does not necessitate a given point of crisis because even if the differences in individual vectors are almost the same, they will diverge.
The key to the crown is that the Lyapunov point will vary according to the changes that are being tracked. That will mean that the zero point of the Lyapunov will change over the course of time even though we can move the center point to the origin for any given measurement. For example, in the color versus black-and-white measurement, the Lyapunov point will be centered on the relative proportion of black and white to color in each given year.
An example of this is the outbreak of World War I. It might seem that the great conflagration was destined to happen. But we can see numerous points where the events might have occurred rather differently, for example, the assassination of Archduke Francis Ferdinand of Austria was not ordained, and in fact the assassination originally failed and then a chance encounter gave Gavrilo Princip (1894-1914) a second attempt which succeeded. If there had been no assassination, then the individuals inside the Austro-Hungarian Empire would not have had the excuse to invade and would probably not have gotten a “blank check” from the German Empire. The motives of the Austro-Hungarian Pro-war party would have been the same, but without the assassination of the heir presumptive Archduke, events would have proceeded differently.
This means that even in a deterministic system, small changes will cause large differences eventually. But remember that the Cultural System still holds because it is in the minds of the population. This means that a crisis occurs because of random events, but the Cultural System is still in crisis not a cause of the random events but because of the contradictions in the logical system. This means that even if some individual crisis point is averted, some other crisis point will occur. This is different from how historical breakpoints are currently used. The difference is that in a mathematical model, one must first find the breakpoints that occur even if the random event is different. For example, even though the European continent was in flux in the summer of 1914, it is entirely possible that the war would not have started or at least started differently. This means that individuals would not have been born and other events would have turned out differently. One of the reasons for this is that the Austro-Hungarians thought that a war could be done against Serbia without involving Russia. The Germans were also convinced that this would take place but not as certainly. However, the Kaiser of Germany left for a three-week vacation indicating that his concerns were minor at best.
This means that the crisis point is still valid even if the exact triggering points will vary. The Cultural System pursued by the heads of Europe indicates that they did not believe that war would be general in nature and therefore the Central Powers were pursuing a strategy that would deal with Serbia without a larger war happening because of it.
But let us return to the math as a decisive factor in interpreting the logical system.
They then found that certain cases need Laplace transforms as opposed to Fourier transforms because some of the effects are not immediately visible. However, the key effect is that the linear systems create Xaos by means of bifurcation. This means that a Cultural System will generate Laplace transformations that use a strange attractor and bifurcate around it. So, because PCA limits the number of important linear algebras to very few, this means that it is possible for a bifurcation to take place.
It is this way in biology and biology is the parent of anthropology and then of history.
But going further, there are many more cycles as far as history is concerned then either biology or anthropology. History means the ability to write things down and have deeper communication with individuals that one does not even know what they are like. In fact, translation means that one does not even know if they speak the authors’ native language. This means that the Xaos theory must be delineated far more closely than has previously been looked at. But that means talking about the nature of Xaos’ theory in a mathematical way.
This means that we have to see that Xaos needs a more solid footing and it needs one which uses.
However, history is more complex when it chooses vectors and may make circular vectors a primary cycle. A trivial example is the payment of rent from an occupant to a landlord which tends to work in two cycles: a yearly one and a monthly one. Clearly these cycles do not correspond with linear motions in the same way that basic vector algebra would like to have. We however were given certain cycles which moved on long-term population lines, with children becoming adults who then had children in their turn. So, we know that a cyclical vector algebra would be coming at least as far as population is concerned.
Further levels of rigor may be explored with a more detailed explanation of whether the order line case is a center, to generate nodes, stars, or other divides.iii This will be dealt with in the next section.
Let us take the Lorenz system and show how it is Xaotic by the two postulates above.
The first step to lay out what is the Lorenz system:
dx/dt = σ(y – z)
dy/dt = x(ρ – z) – y
dz/dt = xy – βz
We can denote:
The key feature of (1) is that a single Lyapunov exponent means that the system is xaotic in the first sense. Because the Lyapunov exponent can be computed by taking the period of the ellipse:
And we can use several methods to determine the Lyapunov exponent including SVD on the three variables or even using Gramm-Schmidt renormalization. If we do it by GSR, then the GSR system creates an orthonormal basis. And that orthonormal basis leads to new initial conditions. But this is recursive which means that if the recursive GSR system produces one Lyapunov exponent, that is sufficient. Since this has already been done with the Lorenz,iv this means that the Lyapunov exponent has been done we can proceed to (2) noting that there is no general solution at the moment. We should also note that a Hopf bifurcation is also plotted.v
It should be noted that the Jacobian is closely related to the Lyapunov exponent, but not quite the same.
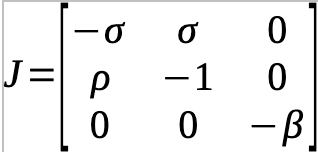
The Jacobian matrix for the Lorenz system at the zero point is:
The next step is to find whether there is a homeomorphism in the Jacobian.
The three tests for a for a homeomorphism are:
There is a one-to-one correspondence between x and y.
The region is continuous.
There is a continuous inverse function which is the identity for x and y or hh-1(x)=x and hh-1(y)=y.
If these are true, then topologically they are equivalent. In a Lorentz Jacobian, there are several shortcuts so that we do not have to prove the general case. Instead, we note that the -β is at least one of the xaotic points and that the
will collapse if we take ρ > 1.
This means that there is a bifurcation at β if ρ>1
Finally, we notice that the pair of fixed points will collapse in a pair if ρ > 1 at β because
or, to put it another way: the x and y will collapse by the 3rd point of homeomorphism if ρ> 1 at β.
This is the root of proving a xaotic system with any set of values.
This means that while the Hartman-Grobman theorem applies, it must still be a translation from words to numbers, and that means that the Cultural System is not quite grounded in a firm science.
But it is getting much closer.
i Andronov, A. A. E. A. Leontovich, I. I. Gordon, and A.G, Maier, 1973. Qualitative Theory of Second-Order Dynamic Systems. Halsted Press.
ii We should note that the Laplace Transform places the weight on the upper end of the transform which is the case of history. It is unsettling that Laplace transforms to do this without having looked at history.
iii Andronov, A. A. E. A. Leontovich, I. I. Gordon, and A.G, Maier, 1973. Qualitative Theory of Second-Order Dynamic Systems. Halsted Press.
iv Frøyland, J., Alfsen, K. H. 1984. Lyapunov-exponent spectra for the Lorenz model. Physical Review A, 29(5), 2928–2931. doi:10.1103/physreva.29.2928, called Frøyland. 2929.
v Frøyland, 2929.