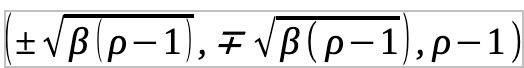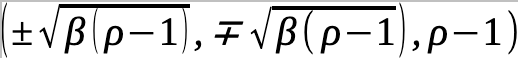Xaotic to Linear
We can see that Xaos in history is about curves differentiated by bifurcations along a zero-value eigenvector. In three dimensions or higher, this means that there are at least three eigenvectors that matter in a Jacobian context: a pair which are the unstable-stable bifurcations and the point which is stable but which is the point where the bifurcation must pass through. So, for example, the first two points are the attractor values, and the last one is the point which the bifurcation must pass through:
The obvious example is any war that is evenly matched or at least somewhat evenly. There is a point where the war is on a knife edge as to whether or not it will be declared. Oftentimes, the war is declared but needs an excuse to happen and the excuse may be waiting for some time before it is actually released. An example would be the First World War, when the armies of Austria-Hungary were waiting for a reason to begin a series of moves that would eventually end up with the two sides at war, that is Serbia and Austro-Hungary. Unfortunately, this was not sufficient to understand the dynamics of what a war would actually bring because Serbia knew that Russia would intervene, and Russia new that France would intervene, and France new that the United Kingdom would intervene once Germany had sided with Austria-Hungary. In other words, the linear space of left versus right between Austria-Hungary and Serbia was inadequate to translate into a European model because the European model had hidden vectors. That in later times we can see these vectors make the problem far more simple, but at the time it was not because the hidden alliances made it from an algebraic vector space to a vector calculus.
Since we can model these as vectors on a vector space, and assigned values which have bifurcated points have two when a given nation will declare war, we can then model when the vector will be crossed. But it is not the vector that instigates more per se but the ρ value which is the actual determining vector.
However, human beings do not model vector spaces in their heads, instead, they use a linear model which is simpler and easier to adapt to the constant changes. This model may be linear from left to right, or it may be planar with two axis. The question therefore is whether there is a root from the coordinate system to the linear model? The answer of course is yes, because the Xaotic form is also on a planar form, though at least it is three-dimensional. That means that the steps must be outlined.
Key Points of Xaos Theory
In mathematics one has to find a linearization of a system which has a Lyapunov exponent. That means that the Lyapunov exponent has a sensitivity to initial conditions.
One can then create a Jacobian matrix to find where the bifurcation divides.
One does this by looking at the disturbance and seeing whether it is topologically equivalent. i
If a set is both typologically equivalent, having a homeomorphism, and transitive, that is having dense orbits on each u,v is infinite, then it is dynamically complex.
However, one also has to look at the way to translate from words that are spoken to objects that can be measured in a Cultural System.
The key concept is to take the 𝜇 and see whether it diverges from 𝜇c.
Circles and Lines
The key reality of Xaos is that there is either a point or a line that catastrophically divides vectors either one way or another. In the Lorenz system, this is a Hopf point whereas in the Mandelbrot set it is a line. There is also the distinction between a stable and an unstable point or line. In the previous section, we looked at the bifurcation of a point and the pair of stable and unstable points that to this send from that.
What this means is that a Hopf bifurcation or a Lyapunov exponent creates a circle or more likely an ellipse around which individuals will cycle. They can be stable, for example, a business arrangement, or unstable, for example, a war. In the previous section we dealt with the Xaos of linear events, but we now have to realize that history is a recursive event and that out of the chaos to form a Xaotic system, individuals then look back at the Xaotic system to form simple generalizations. That means forming a linear or planar representation. In other words, the individuals look back to gauge in a simple manner the complexities that they themselves are living through.
So how do we form a linear or other system? Since the French Revolution, the idea of a left/right dichotomy has been a useful, if imperfect, way of describing it.ii Of course there is an attempt to make planar to account for the difference between “socially” and “economically” in that dichotomy. For example, the Nazi government was socially very reactionary, but was economically quite liberal in certain senses for example marriage was not encouraged only the production of young so-called Aryan babies.
But how does one square this particular circle?
In Xaos theory, we first must look towards PCA and realize that only certain aspects guide the individual into which particular party the individual supports, and that there are exceptions that still mean that the individual is welcome in a particular party. In the 1970s in the United States abortion was still an exception and even in the 2010s it was possible in some cases. This means that we should look at which variables the recursive individuals look at where the dividing line is drawn.
The problem is that the baby boom wants an increase in home values, while younger people want a reduction in home values. We can see that this causes Xaos on both the left and the right: the baby boom left was not going to listen to replacing their old wartime boomer President and thought that his record was extremely strong because he was borrowing money for roadway infrastructure, which they did not need to repay, and the debt was not there problem. On the right, the nominee promised nothing because Trump needed exactly one thing, to be president. Therefore, again because he was old, it did not matter what he promised in order to win the election.
But the larger picture is that the oldest of the boom needed to have all of the levers under their control to make any profits go upwards rather than downwards. This meant that whatever result the election produced it was the older generation that would benefit. The left would benefit by having borrowed money to keep up infrastructure that they themselves used and the right promised the most religious that they could roll back restrictions on teaching their form of religion in school. Because after all, the students could not object for many years.
What this means in mathematical terms is that the right-left paradigm is anchored in three points: the center which is the catastrophic point and the left and right which are the attractors. This means that:
The third point is the catastrophic point and the first and second points will be “left” and “right.” The only step two takes is by flattening out the points and making them a left-right strip by using a transform. The simplest one is the Gram-Schmidt Process taking the catastrophic line of or point as the first point and then the stable line or point as the second and the third as the unstable point. This will need to be repeated as often as possible to get down to the left-right and flatten it to a line.
Hilbert Space as Part of History
To this point, we have used Vector Spaces in a rather marginal way. Now however it becomes time to deal with some larger elephants in the room. One is that Vector Space does not quite have sufficient axioms to suffice. Since we have allowed Laplace Transformations in order to form imaginary results, that is what an individual might do if the circumstances allow it, we must then allow for another individual to represent that imaginary not knowing all of the things that are inside the person’s brain. We must further allow for an unknown individual to be present in a calculation. When this goes on then the state of an individual person becomes infinite, whereas for a Fourier transform, it is still finite because the person has done the act. This means that the rules of linear algebra for a vector space run into the problem that the dimensionality of a given measurement may become infinite since there is an infinite basis. But if this is the case then at infinity the linear algebra rules do not prevent the final total from being outside of the finite total. For example, if t is the final total and the states x are finite then t will be within the vector space of x. but if the states x are infinite then he could be beyond the vector space of x. this is allowed by vector space requirements so another requirement needs to be added to make it so that any total of states that are within a single sector space must also be within that vector space even if they are infinite.
Fortunately, there is the concept of Hilbert space which adds this requirement to vector space and therefore in history, we need to use Hilbert space not just vector space. This means that we need to enumerate further limitations on history vector space both in terms of an individual and in terms of an object or idea that needs to be represented in vector space.
Hilbert Space is defined as a real or complex inner product space that is also a complete metric space with respect to the distance function of the inner product, that is it is a vector space with an inner product that is Cauchy complete, which is the mathematical term for having convergent series of vectors, even if they are infinite, which still resides in the vector space of the states x. This means that any divergent series of vectors will not reside in the vector space, which is appropriate because it still must fill the historical vector space which is not any potential vector space but merely the ones that are possible.
This is so that people who are not known when the measurement occurs can be represented in the aggregate even though they are unnamed. This however means that non-Abelian forms must be vectors in the Hilbert space. An example is the text of a newspaper: the order of letters cannot be transformed into any shape.
The other problem is that we are no longer dealing with Cartesian space but with topology, and again we must make sure that the space does not exceed the maximum. The problem is that we cannot be sure under the conditions set that this will always be true, however, we can add the notion of a Hilbert space. This then does the trick: even with unlimited expansion of terms we know that we will never exceed the limit on the terms. Since there is no reason not to do this, it only becomes necessary to add the Hilbert space to the list of requirements of the Cultural System.
i The Wolfram definition is “A function f is topologically transitive if, given any two intervals U and V, there is some positive integer k such that f^k(U) intersection V!=emptyset.”
ii Bienfait, H. F., and W. E. A. van Beek. 2001. “Right and Left as Political Categories. An Exercise in ‘Not-so-Primitive’ Classification.” Anthropos 96, no. 1: 169–78. http://www.jstor.org/stable/40465460. 169.