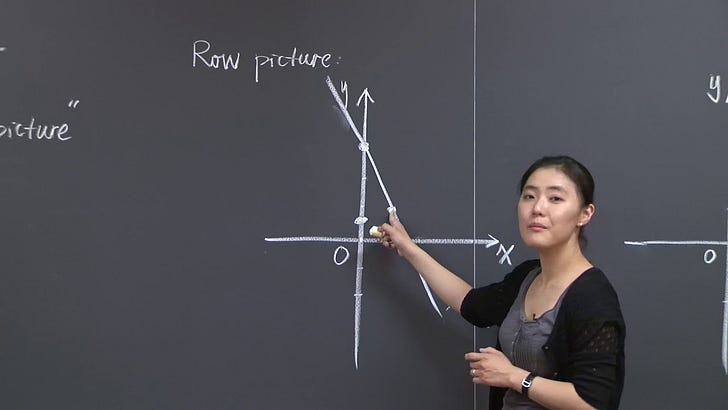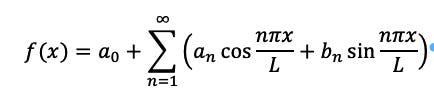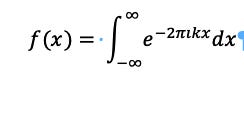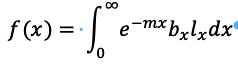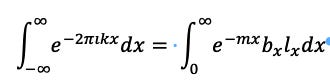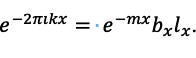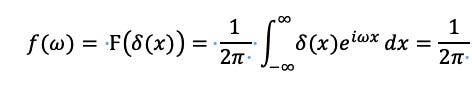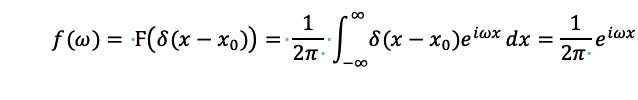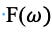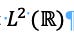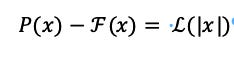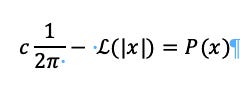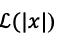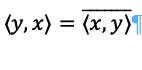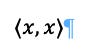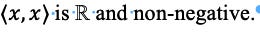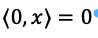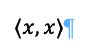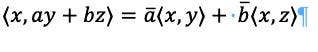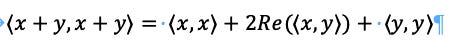Fourier Transforms differ from Laplace Transforms
It is now time to get to the proof that Fourier Transforms differ from Laplace Transforms on republican and democratic shifts.
The first step is to make rigorous the Fourier Transform.
1. A Fourier Transform is a Reimann Integral. It also must have a result if , which in this case is the communication between two entities.
2. We can represent over the interval [-L,L] using the Fourier Series where n is a constant, [-L,L] is the interval over a period of sin and cos:
3. When changing the sum to an interval:
4. In biology this form represents the generational model by Haldane:
Since Haldane notes that in humanity the sex ratio is equal, and we can set
2 𝜋ik to the curve of breeding, this then becomes the Population Pyramid.
Thus
If
It means a biological standpoint the two must be the same.
5. With the addition of an “outside” which contributes members a rate that is analogous to 2 𝜋ik inside, we can then modify the vector chain to a modified Markov Chain with the difference that new entities enter the Markov Chain, while old entities exit by entering into a Markov Chain that self-recurs.
This then is an FT of a Modified Markov Chain with a Markov Matrix as the result because if an arbitrary f is a function that acts as a process transforming X, then G(f) is a block diagonal matrix is equivalent to obtaining the FT of f.
6. So, a new Markov Chain is started by two already established Markov Chains sending a Diracian delta signal. This means that the Haldane function is satisfied in equaling 1.
7. This means that:
And that:
8. Note this means
is not square-integrable because it is at a point, but the delta function is not
.
9. The event that causes reproduction is, however, like the Dirac delta function not well-behaved. (No comment)
10. The difference between the Haldane and the Population Pyramid is that there are constraints on the Population Pyramid for example, money is not a parameter of the Haldane but is in the PP.
11. If this were a Real number then the Population Pyramid would still be a Fourier Transform. If not, then an LT is required.
12. Money is an ℝ. The expectation of Money is an ℝ. But a private expectation not communicated to the other partner is not in ℝ. Thus, the Population Pyramid must have an LT.
13. The Markov Chain, in Particular context cannot be simple. That is be position at L-zero does not contain all of the information that can be ascribed to any particular entity. This can be proven by myriad examples such as Pompei, where people did not know that they were going to die from some external event. This means that classical birth-death Markov chains also do not work because they assume that any new entity is exactly the same as any old entity.
14. This means that the reproduction function is a Poisson Process with the 𝜔 being the time of pregnancy but the longer term is an agreement (or lack thereof) to reproduce with one entity.
15. But this means again that an LT must happen.
16. This means that a generalized FT minus the actual Population Pyramid produces the result of the LT. For example, the difference between the Soviet Union’s predicted FT and the actual.
17. Thus:
Where the L value represents the ℝ of the LT.
18. Since this is a Poisson Process in the Markov Space, therefore:
19. The conjugate of
when added to or multiplied
will result in an ℝ.
20. This means that any FT as a bottom-up number can be checked by calculating the
and adding its complement.
21. While a bottom-up change in the birth rate may be stimulated by an LT on the PP, such as a Depression, it still must go through the Fourier Transform. Thus, the cause may be different from the FT which must be present.
22. The first attempt is the Birth-Death Markov Chain. While, for an FT, this might be sufficient it fails on the LT because the individual birth must include all events. Then Birth-Death Markov Chain is insufficient for a PP because the Total Number does not take into account previous experience which may, or may not, be an ℝ.
23. Thus, we must replace the Simplified BD with one that has each individual member as a separate. Of course, a normal human life span is the Fourier Series which can be shown to be periodicities over the entire “BD span” (though we note that, in our case, it is a conception to death “a span.”) We will call this a Laplace Normal Form.
24. The LPF has the LT in the PP.
25. LNF has experiences for each entity which the CBD model does not have. This leads us to the conclusion that the is more than bottom-up FT changes. This we will call, in the American context, the difference between bottom-up “democratic” and top-down “republican” shifts while turning to middle out elsewhere.
26. This leads to the idea that LT comes from other than bottom-up FT.
27. This means the LPN only increments rather than increments and decrements CBD. Thus, we may use the same FT transforms with a small addition that the number of new entities is drawn from the Dirac delta of existing entities, and for every given country a number of new entries from and to other countries will have the Markov by equal to 0. Tacking λ as the number of new entities and μ as the number of old entities dying:
𝑁(𝑡+Δ𝑡)=𝑁(𝑡)+𝑁(𝑡)λΔ𝑡−𝑁(𝑡)μΔ𝑡
28. ∴ There is a difference between LT and FT which means that both must be used.
Top Down Versus Bottom Up
The difference between the Fourier transform and the Laplace transform in history is that the Fourier transform requires a sender and receiver at least, whereas the Laplace transform can exist only in the mind of a single person. This means that having children is a Fourier transform which may involve many Laplace transforms but is only finalized by the Fourier transform.
This means that at the very least the Fourier transform is bottom-up as the charts in population pyramids show. All too often writers of history confuse the two modes of transformation and they do not understand the differences between Laplace and Fourier transforms. When a movement occurs from the bottom up, it puts pressure on the political leadership because the movement is about the necessities of life. This is different from the top-down, where the direction occurs because imaginary points when squared produce pressure as to how society and politics within that society work. This is not to say that Laplace transforms do not have a bottom-up movement, but they have two manifests at the top of society.
The most obvious example is the American Civil War. The balance between free and slave states was produced by having new states join in equal pairs, and compromises between the free states and slave states, the last of which was 1850. The pressure grew to a point where the supreme court declared that black individuals “had no rights which the white man was bound to respect; and that the negro might justly and lawfully be reduced to slavery for his benefit. He was bought and sold and treated as an ordinary article of merchandise and traffic, whenever profit could be made by it.” This is from the Chief Justice of the Supreme Court of the United States. Looked at mathematically this is saying that any position, even those that are not yet realized, must conform to the statement. This is a Laplace transform and it results in Fourier transforms which are in accordance with it.
In another book, I shall show that Fourier transforms alternate with Laplace transforms, but for now, merely noting the movement of Fourier and Laplace transforms is enough for the present circumstance.
Vector Space Terms
The inner product here means that what mathematicians call a “field” needs to be defined as a space in which the operations of basic arithmetic can be performed. It also means that we need to define what an “inner product” is for the definition of measurements. The inner product is defined as a real or complex vector space where the complex conjugate of a scaler is also scalar.
A field is a set where addition, subtraction, multiplication, and division can be defined as acting as the real numbers in terms of the rational and real numbers.
A scalar is a part of a field that when added, subtracted, multiplied, or divided by a vector produces another vector. So, x and y are scalars which means that v(x,y) is a vector that contains other information than
just the magnitude represented by x and y.
In this case, this means that:
1.
This is called conjugate symmetric of inner product, and it implies that:
is a real number.
This is called conjugate symmetry.
2. In addition to the requirements described in linear algebra, the first variable must be linear.
3. This means that 1 and 2 make the second variable also linear because x is an inner product and is a real number.
4. Is also required that x be positive if (x ,x ) > 0. This is because x is a scaler and negative is part of a vector. That is, you can only have scalars pointing away from the 0 point.
This means that:
1.
2.
3.
iff x = 0.
4.
Which means over ℝ it is bilinear and over ℂ it is Sesquilinear. This means that over ℂ it can be mapped so that an automorphism occurs, that is an isomorphism from the object to itself.
5.
Where Re represents the real part as opposed to the imaginary part. Note that this is similar to binary expansion in algebra.
This addition is similar to quantum mechanics which also requires that the vector space even at an infinite size conforms to the vector space. Since history is part of physics, even though an attenuated version of it, it makes a certain kind of sense. Even though we do not really think of ideas and objects let alone people as moving blobs of quantum fields. It only means that the mathematics conforms to the same requirements. This means that any series of values that history can produce can be encoded as a ket in Dirac’s bra-ket notation. This means that the same proof that bra-ket of functions applies to history. This is left to the reader as an exercise.[i]
It is important to stress that the bra versions of the vectors are column and because we have imaginary vectors in observations, we also must take the complex conjugate. The Ket vectors are rows which means that a Bra-ket vector, leads to a matrix where the columns are in the Bra and the rows are in the Ket or the dot product: <BraT|Ket>.[ii] An example of this would be the chance of a person developing cancer if they smoke. In this case, the Bra is whether they smoke, and the Ket is the chance given which Bra is selected. This means that initially, the chance of developing cancer is the square of the <Bra|Ket>.
This also means that because of Laplace Transforms, we have to introduce the notion that the complex conjugate yields 1 in a <bra|ket> of measurement because no two people can exist at the same place at the same time, even Siamese twins. However, the positional may not be in location but a measurement based on some feature, the example used above is the chance of a person developing cancer. This is important and we shall get back to it in Primary Component Analysis.
With this addition, we can then move to Xaotic structures and find that there is a paradox to which we must resign ourselves. This is the fact that there are so many variables that we must reduce them to a limited number which still holds most of the value. But this reduction in dimensions can be xaotic in its nature, which means that in only a short time the entire Cultural System will diverge even under small initial conditions. That is when some group of people think of something, that is an imaginary component. If they make minor changes to their course of action based on what might have happened, even within the logical system, it may be enough to send results in an arbitrarily large way. We will show that it is this kind of analysis that leads to more distinct alternate histories than looking at a particular meeting. This is because the particular meeting me be already resolved because each member holds a specific view and the meeting is a formality. But going back the reasons that the individuals held their specific view may be fixed at some previous instant and if the previous instance had been different, then the eventual meeting might have had different outcomes.
An example is the declaration of the First World War when a group of leaders of the Austro-Hungarian Empire believed that dealing a significant blow to Serbia was essential for their country to be regarded as a great power. When the Austro-Hungarian Empire asked for permission to invade Serbia, the Germans replied with a statement known as the “blank check.” When analyzing the data from correspondence between the Austro-Hungarian leaders, it becomes clear that the assassination of Franz Ferdinand was envisioned as an opportunity to engage Serbia with the blessing of Germany. This means that the assassination itself was not important it was the fact that it was useful to a certain segment of decision-makers. This means that the meetings after the assassination giving the group of leaders the permission to engage Serbia, even if this was not the case, was the primary motivation. An example is Franz Xaver Josef Conrad von Hötzendorf, who had repeatedly advised his Emperor to go to war with Serbia, but he was countered by Franz Ferdinand. Unfortunately, France Ferdinand was assassinated and Franz von Hötzendorf now had the opportunity to push for war against Serbia.
The Austro-Hungarian leadership was asking for a different blank check than the German leaders were thinking of, but once the blank check was given, leaders of the German Pro-war party were happy to take advantage of it and pushed for their own war, harping on the fact that in the last 50 years that Germany had been victorious over Denmark, Austria, and France which resulted in the formation of the German Empire as the result. Instead of asking whether either the Austro-Hungarian meeting after the assassination was affected or whether the German Empire was going to commit to the blank check is to look too close to the conflict, instead there way forward is to look at how the Balkan situation was dissolved in 1910-1913 and whether or not certain individuals would change their mines if the Balkan situation had been resulting differently. In other words, looking too late leads to erroneous decisions. The is flexible, but it needs time to work.
The First World War, at least as it was fought, could have been avoided, but not quite so close to its beginning. This is because there were many people who saw a change in Europe, and it was better to meet the change now than later. For example, several German generals worried about the construction of Russian railroads because it would mean that the time it would take to mobilize would be shortened. What this means in a Cultural System analysis is that some very powerful people, especially in the military, were watching the same mechanisms of power and wanted to defeat-in-detail the potential threats while there was still time.
Key Points of Vector Spaces:
1. When studying history, it is necessary to learn key terms from linear algebra.
[i] It uses the fact that recovers at the limit of f(x) and g(x).
[ii] T is for Transform which is in Matrix Algebra switch Row to Columns and Columns to Rows. E.g. to