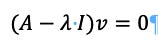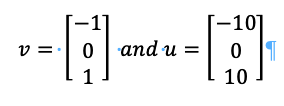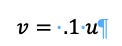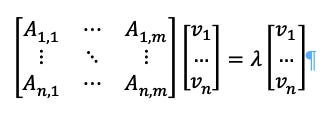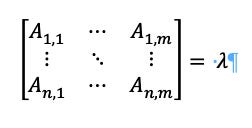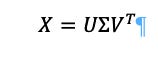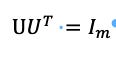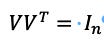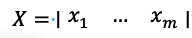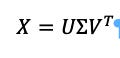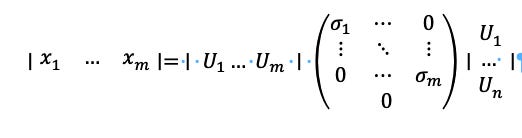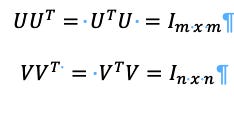Singular Value Decomposition
The first step is to take hundreds or even thousands of individual measurements which have their own dimension and find a lower dimension that maintains all of the data. In this context, the first step is to take the data and do Single Value Decomposition (SVD). This is a step that may make some readers pause and try and follow what is being done. The advantage of doing this is that SVD makes use of strategies that will be useful in performing operations on the data. We learn quite young that addition and subtraction, multiplication, and division are our opposites and that we can, with certain exceptions, reverse the operation of one by its opposite number. We will now learn that SVD has a similar approach just as differentiation and integration do: that is while it is more complex it allows us to do operations that our invertible or have other features that are useful.
Primarily it will take large data with many dimensions and reduce it down to a more manageable set. There are reasons why this is mathematically necessary because first-, second-, third- and fourth-degree equations can be reduced by an algebraic form, but higher dimensions cannot be. This can the proven in a variety of ways but the most common is by Galois representation which proves that there is a new general theory of fifth-degree equations that will solve all of them.
Wanting this is important is that in any given system of equations, one may approximate the map of all of the data to a much simpler map with fewer dimensions. SVD uses techniques from the Fourier transform to do this mapping even if there is no way to exactly approximate it. These techniques will be repeated in further dimension-reducing operations because history is often the search for some measurable quantity that represents an underlying action or belief that does not have a form. It also can find actions that are not on the face of actions or ideas that are not equivalent, but which have deep connections once one looks at the data. This is because very often there will be a great deal of noise with only a few points giving real information. The radio is an excellent example, even very noisy signals can be recognized by only few a few points of data that convey meaning. SVD is often a way to sort through all of the noise to find real data in a particular frame of a logical system. An example would be a cathedral and a castle - they are built with the same techniques but with different objectives. The Gothic cathedral once reached upwards and used glass to let in the sunlight whereas the castle once in light and built stone walls.
So how do we continue?
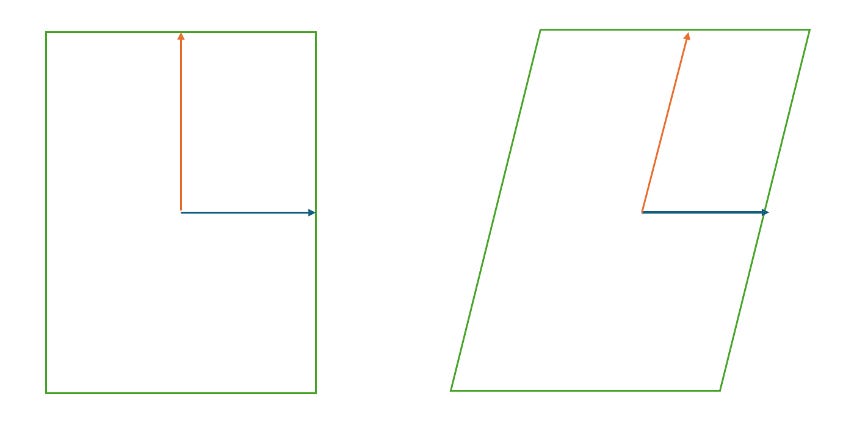
We begin with a visualization:
In the above diagram, the blue line is an eigenvector whereas the orange line is not. This means that we can discover eigenvectors by algebra rather than by geometry because not all eigenvectors are made by drawing.
The next step is to calculate what is called the determinant of the system. This only has a solution if:
Where I is the identity matrix for the system. For example, if:
:
Then 𝜆 would be equal to .1 and:
This can be a matrix not merely a vector, consider Av = 𝜆v:
This means that if:
Then is an eigenvector. This means that if use what is called the determinant (A - λΙ) of we can get the eigenvectors and eigenvalues. This is important because the SVD is among the most important numerical decomposition methods which allows data to be interpreted in a variety of ways. This is used for physics, biology, and other fields and this is why we are taking the time to explain how it is done.
This is because the eigenvector and eigenvalue are key to the SVD in a variety of circumstances. To take an example from history, imagine there is a delegate to some Parliament or Congress. We can surmise from the person’s writing that they are in favor of 21-year-old Freeman being allowed to vote. Is he on the left or the right? The answer is it depends on what time the delegate is elected to. If it is 1800 in America, the delegate would be among the most liberal members of the House of Representatives but in 2000 the delegate would be among the most delegate delicate among the most conservative in fact it would be very unlikely that such a delegate could be elected. If you think about it this is because the definitions of left and right are normally at a specific time, but with eigenvectors, we can look at the long picture. This is what eigenvectors and eigenvalues can do: they can take data from many parliaments or Congress and map the trends over a long period of time.
We do in fact do this, but in language that is not sufficient for measurement. In 1850 the Democratic Party had a large wing that was pro-slavery. How did this change over time? We can take a look at several positions, rate them, and collect data on how individual members voted on them. Then we can take eigenvectors and eigenvalues to look at the long-term movement of a given party. In other words, as biology looks at populations and genetic data, we can look at history and measure how much the mood of the country has changed. This is but one example.
So having shown that characteristic values and characteristic vectors are bound together by definition because a vector must have a length. This means that we can do the reverse, that is instead of taking a matrix and seeing if we can find eigenvalues and eigenvectors, we can take a matrix and reduce the vectors by creating three matrices that will have eigenvalues and eigenvectors in their makeup. The key formula is:
How this works is taking a matrix X and deconstructing the eigenvectors in and using U and V as rotations, with U being columns and VT being rows, with as the rescaling with the diagonals as real non-negative numbers. This means that X can be said to be a matrix of m x n, and the U will be m x m, m x n but everything above m will be zero, and VT will be n x n. The caveat here is that:
and
So, UUT is the identity matrix with m terms and VVT is the identity matrix with n terms because U and V are column vectors while U* and V* are row vectors. This may seem abstruse, so an example seems to be necessary.
Consider an X where the value is the stated desire for independence of a colony. The X can be a number between 0 and 1 on each question which has a bearing on the question of interest, where 0 is devoutly desiring a colony status and 1 is completely desiring independence. For example, it could be that the first question is about cultural allegiance, the second question might be financial, the third might be how relatives of the person are reacting, and so on. This means that we can take an individual person as “x” and label them with a subscript denoting how many people there are, therefore xi, and we can then make each xi have a column or:
Where xi is all of the information concerning x as rows and arrays in columns. What we want to know is what information about a particular person represents their final stance on independence. So, we have a variety of measurements, and we want to know what the final value is.
We start with the idea that X is equal to:
This means that U is columns, and the transpose of V is rows. The 𝛴 is different it has a primary diagonal of numbers and everything below that is 0:
This is the form of the SVD. Which is all well and good, but we have not said how to derive anything useful from it.
The first thing to note about U is that they are “eigen” data points and that they are similar to the X values in their shape. The next feature of U and V is that the columns of U and V are orthonormal and hierarchical. That is when we discover the key features that an individual will want independence, then the U and V will be ordered by the features in order of their importance, and that they will line up orthogonally. Also, remember that both U and V are when composed with the transpose operator equal to the identity with the appropriate subscript and this is both true whichever order takes the transpose. Or:
A similar ordering happens with the Σ in that the σ are aligned diagonally from most to least important.
But how do we order these data points? The answer is because this is history we can look to a Declaration of Independence and see how individuals stood either by election or by revolution. In other words, we have the final value, and we wish to look backward and find the individual components and their relationship to the final value. This will tell us the variance of the data points and see which individuals acted out of the normal valuation and which ones were at variance.
This means that the U values are called the left singular vectors, and the V values are termed the right singular vectors whereas the Σ is the term for the singular values which matches the vector/value distinction that we made above. What this allows us to do is find where the majority of the data is important, and which is less important. That is does the data and metrics conform to the Pareto rule where 20% of the information contains 80% of the value? The means that we do this by ordering from only the first data point and seeing how much variance from the total data, and then going on until we have established that the majority of the information is contained in a few data points. So, if attendance at a meeting gives almost no information in regard to independence, then we can eliminate the attendance at a meeting. Similarly, if we find that purchasing a firearm has a great deal of similarity to the total independence value then we should include that data point. At the end, we will have a much smaller list of data which will keep most of the information that we had on the total population.
This may seem of minor importance, but we have determined which data points are most significant in terms of a final action. And what we will find next is that this SVD will be enlarged by PCA and its descendants to make a more general population. For example, if lack of bread makes the population more amenable to revolt against the government, we can look at various territories and see which ones were vulnerable to revolt. Again, this has been done in words but now we have measurements and more importantly, the different kinds of measurements may be amenable to cross-referencing. For example, which populations are most aligned with the government? For example, we can see that in World War II France that being Catholic was appreciably more prone to support the Vichy lead client state of Nazi Germany. This means that we can ask which other activities Catholicism would be amenable to, for example, believing in the distribution of wealth. This means that we can examine the structure of a country by what things are really important to the populace and which things might have been fissures for members of the population to decide to revolt.
In other words, the SVD is a step towards creating a Cultural System and looking at what components hold the system up. This has the direct consequence that when the components of the Cultural System collapse for a given part of the populace the reasoning of that Cultural System becomes suspect. Because very often how a population changes or an individual changes is important to assessing why revolts and other actions occur, this means that we have a tool that is known to other disciplines and is supported by computer applications such as R, Python, and MATLAB. The ability to look for data that has not been accessed is an important part of history particularly where the events are unknown.
The key feature of SVD is the reduction in the number of data points. Since at a crisis point, fewer and fewer vectors become important, we will see that a marker will be smaller and smaller. The SVD reduces the number of markers in a particular logical system, and we will see that it creates the possibilities of Xaotic changes since we have already demonstrated that the Dirac Delta of population is very small.
But this also means that a general wave of Cultural Systems emerges from the SVD. That is, there is a different wave function for each measurement. This can be represented in a very linear algebra way by the tilt that the Cultural System. For example, that means that an evolutionary mode will be almost straight up because there is an immediate gain, whether economic, cultural, social, or whatever is in question. For example, later on, we will use color television sets versus black and white television sets to formulate the difference between the viewing experience.
But how do we know what shape the parallelogram is? This will depend on the individuals and their sense of time.
Visionary does not overly concern itself with time but with the process of the data. This is because until the individuals can understand the shape of the data there is no reason to bother with time except in the way that time is a process. This means that the shape of other things will take precedence over how to organize time.
Revolutionary, on the other hand, is concerned about time but it is in the nature of the future of time being different than before. This means they cannot look back to a visionary sense of time but to the failures of previous revolutionary movements or partial success. An example would be during the American Revolution, the colony of Massachusetts had evicted many royal governors and set things along different lines. When the United States formed, they looked back to Massachusetts as one of their successes, as well as to the Iroquois Confederacy, and the town and village set up of other colonies. But even in that case, it was a future version of time that was being implemented. This means that time is close at hand which is likened to visionary movements in religion. Indeed, the visionary that is most looked back to is the religious moment when a new idea is set before a body that then reforms the organization along the new idea’s lines. Of course, the most common of which are the revolutionary moments in the beginning of Christianity even though the actual history was different in most respects. That is the revolutionary moment looks back to legendary times and things of the current body of people as being like the revolutionary moments that they wish to emulate.
The change from the revolutionary moment to the evolutionary moment is seen by the fact that the revolutionary moment is seen to be accomplished even if that is only partially true. A good example is the difference between the antebellum United States and the post-Civil War United States: suddenly the exchange of currency for slaves has been all but eradicated though the exchange of labor for goods continues in the form of the Jim Crow system. That is, the exchange of money is almost exclusively held in stocks, bonds, goods, and commodities and the system is reorganized to reflect this organizational shift. For example, agricultural goods were transformed into commodities in the Chicago Board of Trade.
Because of the Whiskey Rebellion (1794), a tax was put on whiskey which was the way to convert corn into two a more tangible good. But when this was not possible the idea of converting corn into beef and pigs was hit upon. Originally Cincinnati was the place where meat was slaughtered and then shipped to the east, and by 1833 Cincinnati had become a center for taking in live animals and converting them into meat.[i] However during the 1840s Chicago went from being a regional center for its own use to a rapidly growing center especially with the introduction of the Michigan Illinois Canal and the Galena and Chicago railway Chicago began to take over first from the other cities in Illinois by about 1852.[ii] The railroads were important for a number of reasons, first because hogs and cattle were made easier to package as components rather than as animals, the second is that once a line was developed it was far easier to move goods continually. By 1861, which it should be noted was a war year, 13 lines originated from Chicago and there were 4600 miles of track.[iii] This meant that the raw products were divided from the distribution from almost the very beginning, because while Chicago was the center for commodities New York was the center for companies and corporations.
We can see then that in the 1830s a visionary form of commodification of corn into a more stable product was starting, but the major introduction of railroads and the commodification of animals into meat was the second step. But it was with the introduction of a trading system that contracts could be signed, and in Chicago’s case, they were future contracts: providing money for the raising and then slaughtering of pork and cattle which then ended up in Chicago itself there to be distributed. This means that we can see the cycle from visionary to revolutionary, to evolutionary. One can mark the increase in production to the Civil War, but the cycle had then started in the 1840s and 1850s long before the war was preordained.
The trigger was not the war itself but the difference between the easterly route over the Great Lakes versus the southerly route along the Mississippi. The advantages of an easterly route were put down systemically in 1860 including damage to agricultural goods from the southern route, the uncertainty of River navigation, the superiority of the railroads in speed, the superiority of New York over New Orleans as a shipping port, and the growth of other outcome cultural goods in New Orleans such as tobacco, cotton, and sugar.[iv] Then there were technical advantages such as the refrigerated railroad car that increased the advantage of the Chicago route as opposed to Cincinnati, St. Louis, and then to New Orleans.[v]
But it is with the future contract that the technical innovations became a solid basis for economic trade: and again it is in the 1850s through the 1870s that the standardization of a “Futures Contract” and “Spot” came to be felt in New York and Chicago.[vi] The difference is in the form of use, which is an important part of any Cultural System: how is the innovation to be made of use, especially in the transition from visionary, to revolutionary, to evolutionary.[vii] This means that time in the evolutionary framework is about time in relationship to the present contract that is being signed, or indeed a future which is uncertain. But that uncertainty means that time is Xaotic from the point of view of a present that does not know exactly what the results are.
However, it is also the past that begins to influence the direction, even in the Revolutionary era. But it is with the evolutionary era that the past becomes a controlling interest in how things are to be done, even if the precedent comes from before, even before the Cultural System existed.
However, it is clear that a theory of the changes needs another book.
Key Points of SVD
1. SVD is key to reducing the basis of a particular matrix.
2. The tilt will be different based on the mode of the system. This will be seen in the bifurcation of the system if present.
3. It will be useful to determine whether the result is Xaotic if this is true.
[i] Hill, Howard Copeland. 1923. “The Development of Chicago as a Center of the Meat Packing Industry.” The Mississippi Valley Historical Review 10, no. 3: 253–73. Called Hill. 253.
[ii] Hill, 258.
[iii] Hill, 260-261.
[iv] Hill, 264-5.
[v] Hill, 270-1.
[vi] Hoffman, G. Wright. 1932. Future Trading upon Organized Commodity Markets in the United States. University of Pennsylvania Press. http://www.jstor.org/stable/j.ctv51318w called Hoffman. 99.
[vii] Hoffman, 109. Hoffman notes that the cash contract is a manufacturing implement whereas the future is to be used as a hedging contract. This means that the cash contract is a legal restriction, not an agricultural requirement.